|
[VIEWED 10488
TIMES]
|
SAVE! for ease of future access.
|
|
|
|
jhyap

Please log in to subscribe to jhyap's postings.
Posted on 08-16-06 5:37
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
n joy :)

|
| |
|
|
|
|
jhyap

Please log in to subscribe to jhyap's postings.
Posted on 08-16-06 5:38
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
.

|
| |
|
|
jhyap

Please log in to subscribe to jhyap's postings.
Posted on 08-16-06 5:38
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
.

|
| |
|
|
jhyap

Please log in to subscribe to jhyap's postings.
Posted on 08-16-06 5:38
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
.
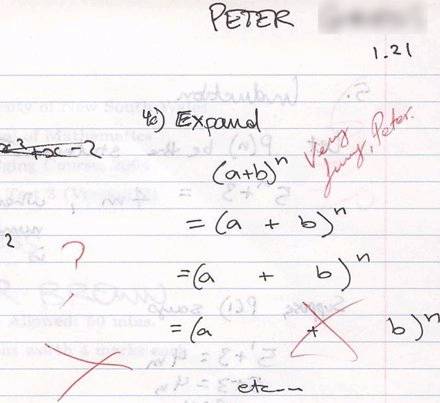
|
| |
|
|
jhyap

Please log in to subscribe to jhyap's postings.
Posted on 08-16-06 5:38
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
.
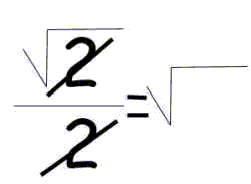
|
| |
|
|
Tyra

Please log in to subscribe to Tyra's postings.
Posted on 08-16-06 5:42
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
ha ha ha ha sachchai funny !!!
|
| |
|
|
jhyap

Please log in to subscribe to jhyap's postings.
Posted on 08-16-06 5:51
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Theorem : 3=4 Proof: Suppose: a + b = c This can also be written as: 4a - 3a + 4b - 3b = 4c - 3c After reorganising: 4a + 4b - 4c = 3a + 3b - 3c Take the constants out of the brackets: 4 * (a+b-c) = 3 * (a+b-c) Remove the same term left and right: 4 = 3 Theorem : All numbers are equal to zero. Proof: Suppose that a=b. Then a = b a^2 = ab a^2 - b^2 = ab - b^2 (a + b)(a - b) = b(a - b) a + b = b a = 0 Theorem: 1$(dollar) = 1c(cent). Proof: And another that gives you a sense of money disappearing... 1$ = 100c = (10c)^2 = (0.1$)^2 = 0.01$ = 1c Theorem: 1 = -1 . Proof: 1/-1 = -1/1 sqrt[ 1/-1 ] = sqrt[ -1/1 ] sqrt[1]*sqrt[1] = sqrt[-1]*sqrt[-1] ie 1 = -1 Theorem: 4 = 5 Proof: 16 - 36 = 25 - 45 4^2 - 9*4 = 5^2 - 9*5 4^2 - 9*4 + 81/4 = 5^2 - 9*5 + 81/4 (4 - 9/2)^2 = (5 - 9/2)^2 4 - 9/2 = 5 - 9/2 4 = 5 hehe provin some theorem... challenge ur professors :)
|
| |
|
|
jhyap

Please log in to subscribe to jhyap's postings.
Posted on 08-16-06 5:53
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Theorem 0/0 = 4 0/0 = (4-4)/(2-2) = ((2+2)(2-2))/(2-2) since 4 = 2^2 and a^2-b^2 = (a+b)(a-b) = (2+2) = 4 Proved :)
|
| |
|
|
bidhan40

Please log in to subscribe to bidhan40's postings.
Posted on 08-16-06 6:09
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
jhyap your logic of 3=4 is wrong. because from the question it is given a+b= c i.e a+b-c=0 while solving the equation you did (a+b-c)/(a+b-c) =1 which is wrong . as 0 divide by 0 can never be equal to 1. while making the eqaution you can never give such equations as it is against the rule of algebra.
|
| |
|
|
rein

Please log in to subscribe to rein's postings.
Posted on 08-16-06 6:17
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
3=4 Proof: Suppose: a + b = c This can also be written as: 4a - 3a + 4b - 3b = 4c - 3c After reorganising: 4a + 4b - 4c = 3a + 3b - 3c Take the constants out of the brackets: 4 * (a+b-c) = 3 * (a+b-c) Remove the same term left and right: 4 = 3 This is wrong because u cannot divide by a+b-c which is 0 (since a+b=c) Theorem : All numbers are equal to zero. Proof: Suppose that a=b. Then a = b a^2 = ab a^2 - b^2 = ab - b^2 (a + b)(a - b) = b(a - b) a + b = b a = 0 This is wrong because u cannot divide by a-b coz a-b=0 (u assumed a=b) Theorem: 1$(dollar) = 1c(cent). Proof: And another that gives you a sense of money disappearing... 1$ = 100c = (10c)^2 = (0.1$)^2 = 0.01$ = 1c This is wrong because (10c)^2 is not equal to (0.1$)^2 Theorem: 1 = -1 . Proof: 1/-1 = -1/1 sqrt[ 1/-1 ] = sqrt[ -1/1 ] sqrt[1]*sqrt[1] = sqrt[-1]*sqrt[-1] ie 1 = -1 This is wrong because sqrt[ x/y] is not equal to sqrt[x]/sqrt[y] Theorem: 4 = 5 Proof: 16 - 36 = 25 - 45 4^2 - 9*4 = 5^2 - 9*5 4^2 - 9*4 + 81/4 = 5^2 - 9*5 + 81/4 (4 - 9/2)^2 = (5 - 9/2)^2 4 - 9/2 = 5 - 9/2 4 = 5 This is wrong because (a-b)^2 i=(x-y)^2 doesnot mean a-b=x-y if, for example. a-b is positive and x-y is negative 0/0 = 4 0/0 = (4-4)/(2-2) = ((2+2)(2-2))/(2-2) since 4 = 2^2 and a^2-b^2 = (a+b)(a-b) = (2+2) = 4 Proved :) This is wrong because u cannot 0/0 is not 1 ( as u canceled (2-2)/(2-2))
|
| |
|
|
rein

Please log in to subscribe to rein's postings.
Posted on 08-16-06 6:20
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
oops , read last line as This is wrong because 0/0 is not 1 (as u canceled (2-2)/(2-2))
|
| |
|
|
jhilke_

Please log in to subscribe to jhilke_'s postings.
Posted on 08-16-06 6:28
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Jhyap, very funny. Keep it coming. You must be smoking/drinking some good stuff :) Rein, brilliant. now i know that math can be deceitful
|
| |
|
|
hyperthread

Please log in to subscribe to hyperthread's postings.
Posted on 08-16-06 6:29
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Jhyap on Theorem: 1$(dollar) = 1c(cent). Proof: And another that gives you a sense of money disappearing... 1$ = 100c = (10c)^2 <<<<<<<<<<<<<<<<< FLAW>>>(10c)^2 = 100c^2 != 100c = (0.1$)^2 = 0.01$ = 1c <<<<<<<<<<<
Theorem: 4 = 5
Proof:
16 - 36 = 25 - 45
4^2 - 9*4 = 5^2 - 9*5
4^2 - 9*4 + 81/4 = 5^2 - 9*5 + 81/4
(4 - 9/2)^2 = (5 - 9/2)^2 <<<<<<<<<<>>>>>>> 2*4*9/2 =72/2 !=81/2
4 - 9/2 = 5 - 9/2
4 = 5 <<<<<<<<<<<<<<<<<<
heorem 0/0 = 4
0/0 = (4-4)/(2-2) = ((2+2)(2-2))/(2-2) <<<0/0 is undefined (its not infinity) use <<<<<<<<<<<<<<<<<<<<<<<<<<< since 4 = 2^2 and a^2-b^2 = (a+b)(a-b)
= (2+2) = 4 <<<<<<<<<<<<<<<<< but not = 0
Proved :)
|
| |
|
|
hyperthread

Please log in to subscribe to hyperthread's postings.
Posted on 08-16-06 6:32
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Theorem 0/0 = 4 0/0 = (4-4)/(2-2) = ((2+2)(2-2))/(2-2) <<< use L'Hopitals rule since 4 = 2^2 and a^2-b^2 = (a+b)(a-b) = (2+2) = 4 Proved :)
|
| |
|
|
jhyap

Please log in to subscribe to jhyap's postings.
Posted on 08-16-06 9:32
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
l'hopital's rule :) take derivitives :)
|
| |
|
|
GreenMapleTree

Please log in to subscribe to GreenMapleTree's postings.
Posted on 08-16-06 9:44
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
We are here for some fun! we have all seen those funny math in our high school. We do not want to understand those math, we just want to have some fun. Who cares!!! Sara maja kir kira bhayo...
|
| |
|
|
somewhereinUSA

Please log in to subscribe to somewhereinUSA's postings.
Posted on 08-16-06 9:48
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Really Funny. Specially # 3 is hilarious. Thanks a lot.
|
| |
